Базовые принципы предиктивного управления
В Российской практике внедрения большинство СУУТП представлены системами класса APC (Advanced Process Control). APC объединяет в себе две ключевые методологии управления:
- Model Predictive Control (MPC) – предиктивное управление процессом на основе его динамической модели,
- Advanced (Enhanced) Feedback Control Techniques – методы усовершенствованного управления с обратной связью:
- Time-Delay Compensation Control – управление с компенсацией запаздывания,
- Inferential (Soft Sensing) Control – управление на основе показаний виртуальных анализаторов качества,
- Selective/Override Control – селективное управление, управление с ограничениями в системе,
- Nonlinear Control – нелинейное управление,
- Adaptive Control – адаптивное управление.
Основой APC является многопараметрический контроллер MPC. Большинство APC имеют в своем составе виртуальные анализаторы и реализуют управление с запаздыванием и ограничениями. Лишь некоторые «продвинутые» APC последнего десятилетия отличаются наличием элементов нелинейного и/или адаптивного управления. При этом каждое отдельно взятое решение Advanced Feedback Control Techniques может быть реализовано автономно на платформе программного обеспечения РСУ, что в некоторых случаях является достаточной и эффективной альтернативой сложной APC. Это обстоятельство подчеркивает актуальность процедуры комплексного предварительного обследования технологического процесса на предмет целесообразности внедрения методов и систем усовершенствованного управления.
Базовыми компонентами MPC являются:
- Многопараметрическая динамическая модель, связывающая входные переменные процесса с выходными , при этом входными являются управляющие параметры (MV) и измеримые возмущения (DV), а выходными – контролируемые параметры (CV);
- Алгоритм расчета целевых значений CV при наличии ограничений в системе;
- Алгоритм предиктивного управления с обратной связью, на основе которого контроллер обеспечивает минимальное отклонение выходной переменной от целевого значения на горизонте планирования, исключая чрезмерное изменения величины управления (MV).
Многопараметрическая динамическая модель контроллера строится на основе экспериментальных данных, получаемых в ходе тестирования промышленной установки. Тестирование реализуется либо методом ступенчатого воздействия, либо методом псевдослучайной двоичной последовательности. В первом случае в ходе теста осуществляется изменение величины MV на 1-5 % от текущего эксплуатационного значения. Во втором – в течение некоторого интервала времени MV последовательно принимает верхнее и нижнее значения, отклоняясь от текущего на равную величину. В обоих случаях строится кривая отклика контролируемой величины, характеризующая реакцию CV на изменение MV или DV в дискретные моменты времени.
По данным кривой отклика может быть построена одна из дискретных моделей:
Finite Impulse Response (FIR) – конечная импульсная характеристика:
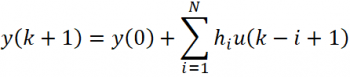
или Finite Step Response (FSR) – конечная ступенчатая характеристика:
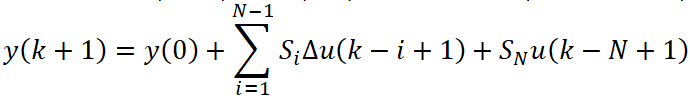
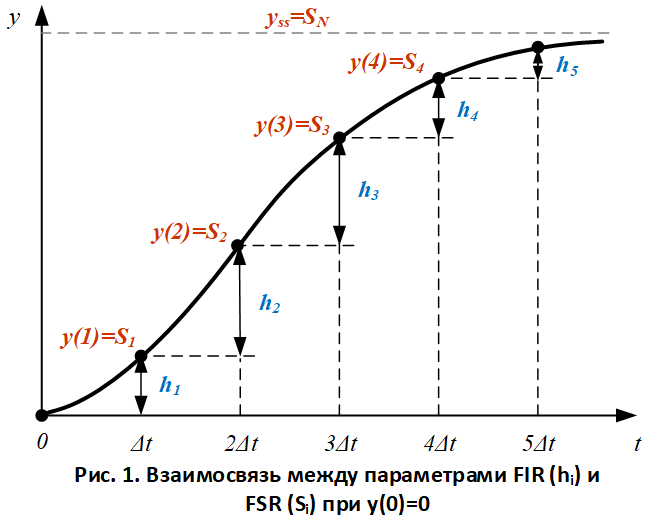
Параметрами моделей являются коэффициенты и связанные между собою (рис. 1), что позволяет вывести FIR из FSR и наоборот. Согласно модели FIR выход y определяется абсолютными значениями входной переменной u, а в случае FSR – изменениями 
. Количество тактов дискретизации N и шаг дискретизации 
выбираются таким образом, чтобы произведение 
не было меньше времени достижения выходом y нового установившегося значения 
(времени переходного процесса).
Важной особенностью обоих моделей является возможность вычисления последующего значения выхода y(k+1) на основе значений входной величины в предыдущие дискретные моменты времени, т.е. возможность прогнозирования значения y в будущем. Кроме того, прогнозирование осуществляется с учетом запаздывания в системе.
Контроллер МРС является многопараметрическим и многосвязным, следовательно, в отличии от САУ, состоящей из множества несвязанных контуров регулирования, в MPC учитывается то, что одна переменная MV может влиять на несколько CV и в то же время одна CV может зависеть от нескольких MV. Введя допущение о линейности процесса и используя принцип суперпозиции, составим FSR для случая, когда в системе два входа u1 и u2 и два выхода y1 и y2. Тогда прогнозные значения для выходных параметров при y1(0)=y2(0)=0:
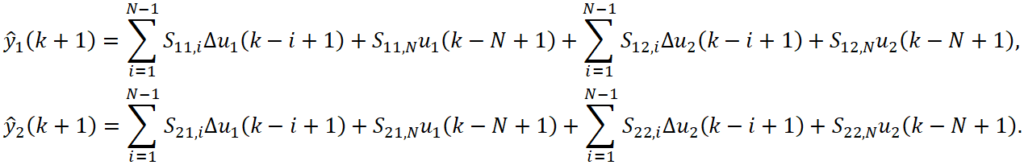
Другой особенностью дискретных моделей является возможность их корректировки в онлайн режиме с помощью процедуры Output Feedback and Bias Correction (коррекция смещения на основе обратной связи). В модель вводится величина отклонения прогнозного значения от фактического в k-ый момент времени. Корректный прогноз в (k+1)-ый момент примет вид:
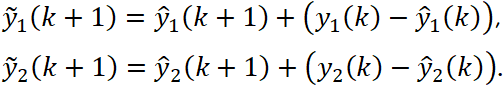
Дискретные модели преобразуются в параметрические в виде передаточных функций. Как правило, используются передаточные функции первого и второго порядков. Множество передаточных функций образуют матрицу динамических связей. Графически такую матрицу представляют в виде совокупности кривых отклика и соответствующих коэффициентов усиления (Gain коэффициентов).
рис. 2 представлен пример матрицы для процесса ректификации при трех входных параметрах (MV1 – расход греющего пара в кипятильник колонны, MV2 – расход флегмы, DV1 – расход питания колонны) и четырех выходных (CV1 – концентрация низкокипящего компонента в дистилляте, CV2 – перепад давления в колонне, CV3 – температура куба колонны, CV4 – концентрация низкокипящего компонента в кубовом остатке).
Алгоритм расчета целевых значений CV при наличии ограничений в системе основан на применении статической модели процесса, которая может быть получена путем преобразования динамической модели и представлена, в частности, системой линейных уравнений:
или с учетом коррекции смещения
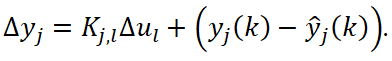
В ходе реализации алгоритма решается оптимизационная задача №1, в которой определяются целевые значения CV 
и соответствующие уставки MV 
, обеспечивающие в дискретные моменты времени минимум/максимум критерия эффективности. Если критерий имеет линейную форму, то используется метод линейного программирования, если же критерий задан в квадратичной форме – метод квадратичного программирования. В частном случае критерий имеет вид:
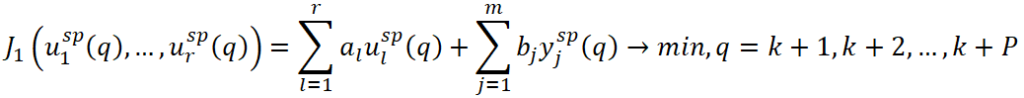
при ограничениях в системе:
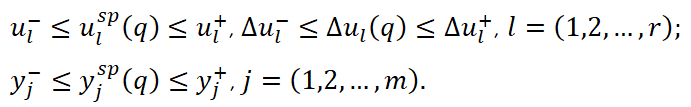
Весовые коэффициенты
задаются специалистами планово-экономической и производственно-технической служб исходя из экономической конъектуры и приоритетности MV, CV. Своевременное определение весовых коэффициентов экономического характера для отдельного процесса или установки в составе производства может оказаться сложной задачей, что приводит к исключению из критерия J1 экономической составляющей. В этом случае решающая роль отводится весовым коэффициентам, определяющим приоритет между параметрами. В частности, критерий может быть приравнен одному из CV (выход продукта, концентрация ключевого параметра на выходе и т.д.) или MV (расход теплоносителя, расход реагента и т.д.).
Особое значение в работе алгоритма отведено наличию или отсутствию системы более высокого уровня Real-Time Optimization (RTO). Если система RTO внедрена на производстве, то критерий J1 при тех же ограничениях принимает иной вид:
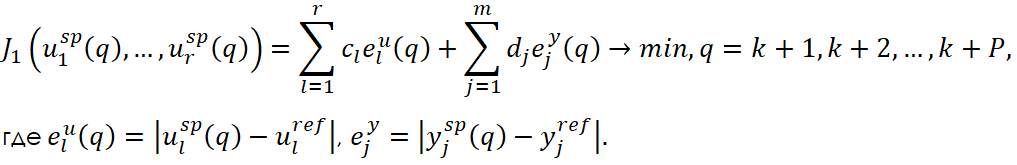
Величины 
– весовые коэффициенты, 
– рекомендуемые уставки, рассчитываемые RTO после достижения процессом стационарного состояния (неизменности параметров во времени). остаются постоянными в течение всего периода стационарности. В основе расчета используется имитационная модель и экономические показатели производства в целом, что позволяет RTO координировать одновременную работу комплекса контроллеров APC. Имитационная модель RTO не учитывает динамические особенности поведения отдельных процессов, такие как запаздывание, колебательность переходного процесса, наличие шумов измерения и т.д. Более того, стационарность обусловлена рядом допущений. Таким образом, расчет контроллером MPC величин 
в дискретные моменты времени обоснован реальной динамикой процесса и необходимостью обеспечения устойчивости системы, а их приближение к является стратегической экономической задачей в контексте всего производства.
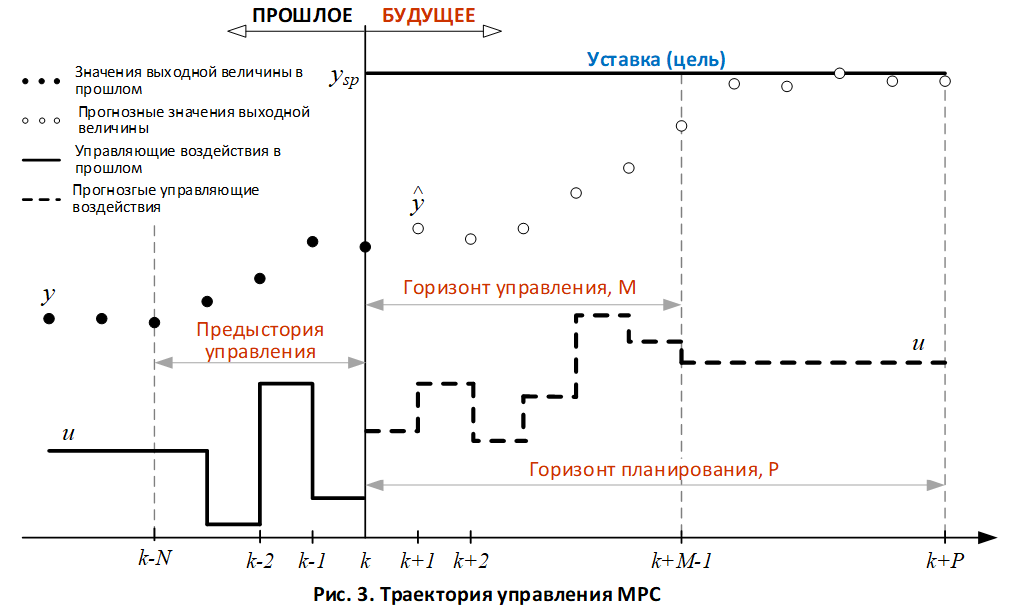
Алгоритм предиктивного управления с обратной связью рассчитывает последовательность управляющих переменных 
, обеспечивающую достижение контролируемыми величинами целевых значений на горизонте управления (рис. 3).
Рассмотрим частный случай построения траектории управления для одной выходной переменной при единственном управлении .
Для расчета используется динамическая модель со смещением. Несмотря на то, что осуществляется расчет управления для М-1 дискретных моментов в будущем, контроллер реализует лишь управление на k+1 такте. Это необходимо для последующего внесения в модель корректировки смещения по результатам измеренного y(k+1).
Представим прогнозные значения выходной переменной на горизонте планирования P в дискретный момент времени k, для которого известно фактическое значение y(k). Последующие фактические значения выхода неизвестны, поэтому прогноз строится с учетом смещения лишь в k-ый момент:
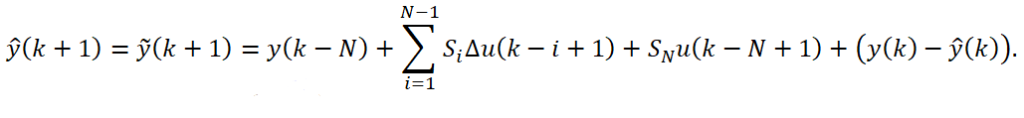
В расчете прогноза 
осуществляется сдвиг на один временной такт предыстории управления: выводится точка 
, в результате чего начальным моментом становится 
. При этом неизвестное конечное изменение управления 
при i=1 под знаком суммы принимается 
. Тогда:
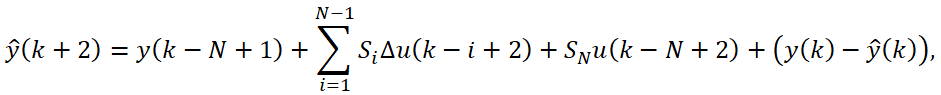
и т.д. до окончания горизонта планирования:
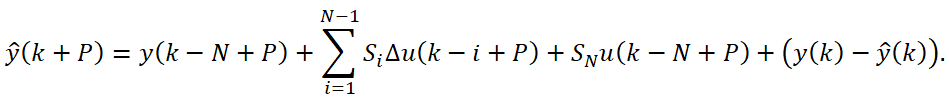
Траектория достижения контролируемой величиной CV целевого значения 
на горизонте планирования P должна быть оптимальной. Важно не только быстро достичь целевого значения, но и предотвратить существенное изменение манипулируемого параметра. С этой целью в каждый дискретный момент времени после расчета горизонта планирования строится горизонт управления 
. Решается оптимизационная задача №2, в которой критерий оптимизации имеет вид:
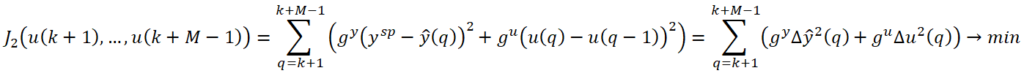
при ограничениях:
Весовые коэффициенты 
, задаются исходя из приоритетности входных и выходных переменных с учетом требования устойчивости процесса.
Далее реализуется оптимальное управление только лишь в k+1-ый момент 
, измеряется фактическое и строится новый прогноз на горизонте P:
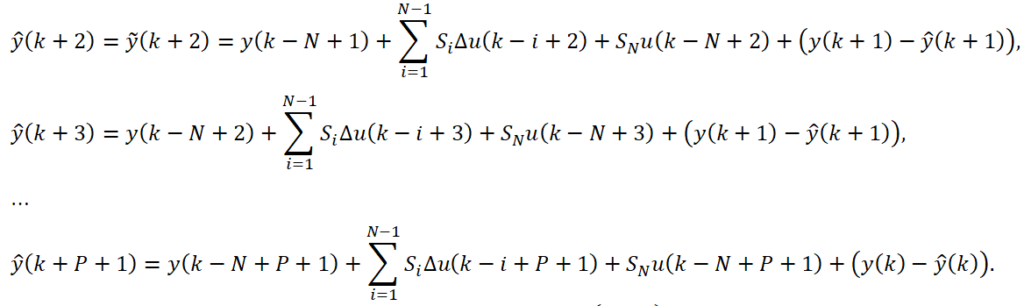
После определяется горизонт управления, реализуется 
и т.д.
В общем случае, когда процесс характеризуется множеством входных 
и выходных переменных 
, после расчета горизонта планирования для всех выходных переменный строится горизонт управления 
, В этом случае критерий 
принимает вид:
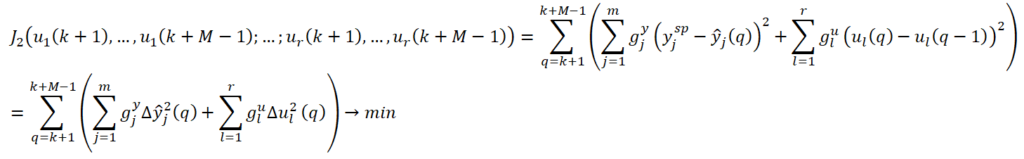
при ограничениях
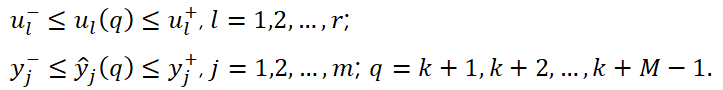
Особо необходимо обратить внимание на выбор величин горизонтов управления и планирования. Увеличение горизонта управления M делает контроллер MPC более агрессивным и существенно увеличивает объем вычислений. Как правило, величина M выбирается в диапазоне 
. Уменьшение горизонта планирования P также делает контроллер более агрессивным. Величина P выбирается больше M с целью оценки поведения 
по истечению горизонта управления при постоянном последнем 
. Горизонт принимает значение P=M+N.
Увеличение горизонта планирования на величину N позволяет оценить весь отклик CV на последнее изменение 
.